Hukum Pascal

Hukum Pascal dinyatakan oleh seorang filsuf sekaligus ilmuwan Prancis, Blaise Pascal (1623-1662) menyatakan bahwa:

“Jika tekanan eksternal diberikan pada sistem tertutup, tekanan pada setiap titik pada fluida tersebut akan meningkat sebanding dengan tekanan eksternal yang diberikan.”

Hukum Pascal ini menggambarkan bahwa setiap kenaikan tekanan pada permukaan fluida, harus diteruskan ke segala arah fluida tersebut. Hukum pascal hanya dapat diterapkan pada fluida, umumnya fluida cair.

Rumus Hukum Pascal

Rumus hukum Pascal dalam sistem tertutup dapat disimpulkan dengan:

$P_{keluar} = P_{masuk}$

Agar lebih simpel, formula diatas ditulis dengan 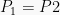$P_1 = P2$

Seperti yang sudah kita tahu bahwa tekanan adalah gaya dibagi besar luasan penampangnya (P = F/A), maka persamaan diatas dapat ditulis kembali sebagai berikut:

$\frac{F_2}{A_2} = \frac{F_1}{A_1}$

Atau

$\frac{F_2}{F_1} = \frac{A_1}{A_2}$

Besarnya keuntungan mekanis dari sistem fluida/hidrolik yang menggunakan hukum Pascal dapat diketahui dari rasio gaya yang keluar dibagi gaya yang diberikan.

$keuntungan mekanis = \frac{F_2}{F_1}$

Karena luasan penampang berbanding lurus dengan gaya, maka keuntungan mekanis juga dapat langsung diketahui dari rasio kedua luasan penampang.

Perhatikan gambar mekanisme hidrolik diatas. Karena cairan tidak dapat ditambahkan ataupun keluar dari sistem tertutup, maka volume cairan yang terdorong di sebelah kiri akan mendorong piston (silinder pejal) di sebelah kanan ke arah atas. Piston di sebelah kiri bergerak ke bawah sejauh h1 dan piston sebelah kanan bergerak ke atas sejauh h2. Sesuai hukum Pascal, maka:

$A_2h_2 = A_1h_1$

Sehingga,

$\frac{A_2}{A_1} = \frac{h_1}{h_2}$

Penerapan Hukum Pascal

Hukum Pascal banyak diterapkan untuk memudahkan pekerjaan manusia. Salah satu contoh yang paling sederhana adalah pengungkit hidrolik. Pada pengungkit hidrolik, sedikit gaya masuk yang diberikan digunakan untuk menghasilkan gaya keluar yang lebih besar dengan cara membuat luasan piston bagian luar lebih besar daripada luasan piston bagian dalam. Dengan cara ini, keuntungan mekanis yang didapatkan akan berlipat ganda tergantung rasio perbedaan luasan piston. Sebagai contoh, jika luasan piston luar 20 kali lebih besar daripada piston bagian dalam, maka gaya yang keluar dikalikan dengan faktor 20; sehingga jika gaya yang diberikan setara dengan 100 kg, maka dapat mengangkat mobil hingga seberat 2000 kg atau 2 ton.

Contoh lainnya adalah rem hidrolik pada mobil seperti yang dapat dilihat pada gambar dibawah. Ketika pengemudi menginjak pedal rem, tekanan pada silinder utama akan meningkat. Kenaikan tekanan ini akan diteruskan keseluruh bagian fluida di sepanjang sistem hidrolik sehingga silinder rem akan mendorong kanvas rem terhadap cakramyang menempel pada roda mobil. Akibat gesekan antara kanvas rem dengan cakram akan menyebabkan laju mobil berkurang. Rem hidrolik seperti ini biasa disebut rem cakram dan digunakan pula di sepeda motor. Fluida yang digunakan sebagai media penyalur tekanan adalah oli.

Dapat dikatakan bahwa semua sistem hidrolik menggunakan hukum Pascal. Sistem hidrolik dipakai di seluruh kendaraan berat, mesin pengangkut, pabrik-pabrik, dan semua peralatan yang membutuhkan gaya yang besar menggunakan sistem hidrolik karena keuntungan mekanisnya yang cukup tinggi dan sistem kerjanya yang sederhana.

Contoh Soal Hukum Pascal

Contoh Soal 1

Sebuah pengungkit hidrolik digunakan untuk mengangkat mobil. Udara bertekanan tinggi digunakan untuk menekan piston kecil yang memiliki jari-jari 5 cm. Takanan yang diterima diteruskan oleh cairan didalam sistem tertutup ke piston besar yang memiliki jari-jari 15 cm. Berapa besar gaya yang harus diberikan udara bertekan tinggi untuk mengangkat mobil yang memiliki berat sebesar 13.300 N? Berapa tekanan yang dihasilkan oleh udara bertekanan tinggi tersebut?

Pembahasan:

Dengan menggunakan rumus hukum Pascal $F_2/A_2 = F_1A_1$ dapat dicari nilai gaya yang diperlukan:

$F_1 = (\frac{A_1}{A_2})F_2$

Sehingga didapat:

$F_1 = \frac{\pi (5 \times 10^{-2} m)^2}{\pi (`5 \times 10^{-2} m)^2} (13.300 N)$

$F_1 = \frac{25}{225} (13.300 N)$ = 1.480 N[/latex]

Kemudian, banyaknya tekanan udara yang dibutuhkan sebesar:

$P_1 = \frac{F_1}{A_1} = \frac{1.480N}{\pi (15 \times 10^{-2} m)^2}$ $P_1 = 188.000 Pa$

Besarnya tekanan yang diperlukan, hampir dua kali besar tekanan atmosfer.

Contoh Soal 2

Sebuah pengungkit hidrolik memiliki piston masuk (utama) dengan diameter 1 cm dan silinder luar dengan diameter 6 cm. Tentukan gaya yang dikeluarkan oleh silinder luar ketika diberikan gaya sebesar 10 N pada silinder masuk. Jika piston masuk bergerak sejauh 4 cm, seberapa jauh piston luar bergerak?

Pembahasan:

Dengan menggunakan rumus hukum Pascal $F_2/A_2 = F_1A_1$ dapat dicari nilai gaya yang dihasilkan: